本次学习我们将详细介绍Apriori关联规则算法中的相关概念和，Apriori算法过程推导。

ps：本文参考的博客链接有如下，博主先行感谢。
(https://www.cnblogs.com/pinard/p/6293298.html)
(https://www.cnblogs.com/chaoren399/p/4870288.html)

一、基本概念

a) 支持度：关联规则A=>B的支持度指的是事件AB同时发生的概率
$$Support(A=>B) = P(A {\cup} B)$$
b) 置信度：关联规则A=>B的置信度指的是在A发生的基础上发生B的概率
$$Confidenc(A=>B) = P(B|A)$$

举个例子，在购物数据中，纸巾对应鸡爪的置信度为40%，支持度为1%。则意味着在购物数据中，总共有1%的用户既买鸡爪又买纸巾;同时买鸡爪的用户中有40%的用户购买纸巾。
c) K项集
如何事件A包含k个元素，那么称这个事件为k项集，并且事件A满足最小支持度阈值的事件称为频繁k项集。（说明这个事件在所有情况里发生的比较多）
d) 由频繁项集产生强关联规则
1） $k$维数据项集$L_k$是频繁项集的必要条件是它的所有$k-1$维子项集也为频繁项集，记为$L_(k-1)$。
2）如果$k$维数据项集的任一一个$L_(k-1)$不是频繁项集，则$L_k$本身也不是最大数据项集。
3） $L_k$是$k$维频繁项集，若所有$k-1$维频繁项集$L_(k-1)$中包含$L_k$的$k-1$维子项集的个数小于$k$，则$L_k$不可能是$k$维最大频繁数据项集。
4）同时满足最小支持度阈值和最小置信度阈值的规则称为强规则。

二、Aprior算法过程

目标一：找最大k项频繁项集：根据支持度

输入：数据集D，支持度阈值α
输出：最大k项频繁集

1) 扫描整个数据集D，得到所有出现过的数据，作为候选频繁项集。k=1，频繁0-项集为空集。
2) 挖掘频繁k-项集
a) 扫描数据计算候选频繁k项集的支持度
b) 去除候选中支持度低于阈值的数据集，得到频繁k项集。若为空，则返回k-1项集为结果，算法结束；若只有一项，则返回频繁k-项集为结果，算法结束。
c) 基于频繁k项集，连接生成候选频繁k+1项集。
3）令k=k+，转2）。

下面举个例子看看；

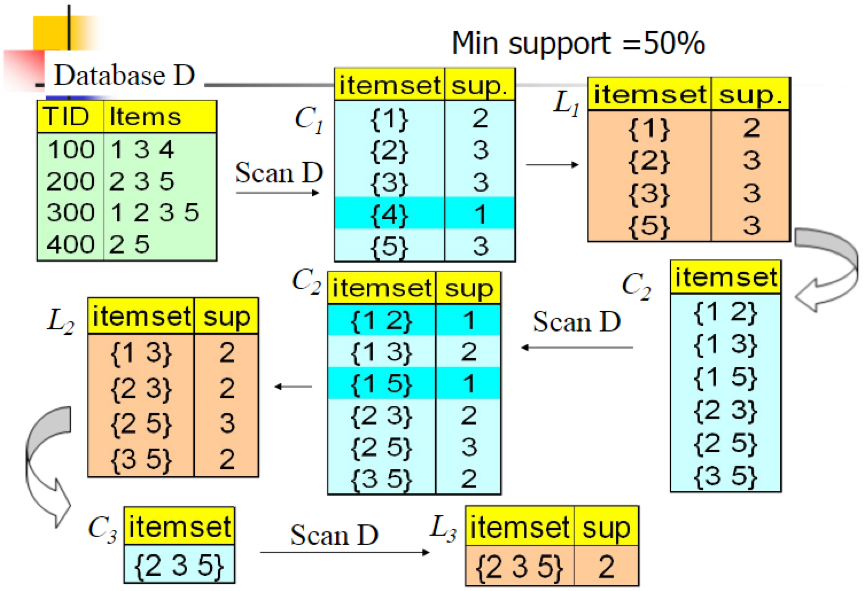
我们的数据集D有4条记录，分别是134,235,1235和25。现在我们用Apriori算法来寻找频繁k项集，最小支持度(支持度阈值)设置为50%。首先我们生成候选频繁1项集，包括我们所有的5个数据并计算5个数据的支持度，计算完毕后我们进行剪枝，数据4由于支持度只有25%被剪掉。我们最终的频繁1项集为1235，现在我们链接生成候选频繁2项集，包括12,13,15,23,25,35共6组。此时我们的第一轮迭代结束。
进入第二轮迭代，我们扫描数据集计算候选频繁2项集的支持度，接着进行剪枝，由于12和15的支持度只有25%而被筛除，得到真正的频繁2项集，包括13,23,25,35。现在我们链接生成候选频繁3项集,123, 125，135和235共4组，这部分图中没有画出。通过计算候选频繁3项集的支持度，我们发现123,125和135的支持度均为25%，因此接着被剪枝，最终得到的真正频繁3项集为235一组。由于此时我们无法再进行数据连接，进而得到候选频繁4项集，最终的结果即为频繁3三项集235。

目标二：由频繁项集（不仅仅是最大频繁项集）产生关联规则：根据置信度

输入：频繁项集
输出：关联规则

1) 扫描每个频繁项集（从最大频繁项集向下扫描），排列组合构建规则
2) 计算规则的置信度是否大于置信度阈值，若大于则记录下来，若小于则抛弃。

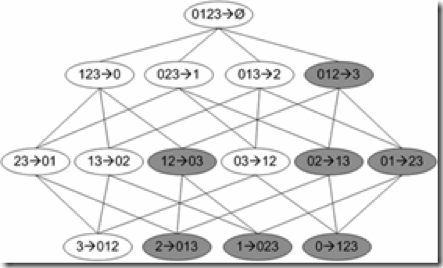
（抛弃的优化：如下图所示）

图中给出了从项集{0,1,2,3}产生的所有关联规则，其中阴影区域给出的是最低可信度的规则。可以发现如果{0,1,2}->{3}是一条低可信度规则，那么所有其他以3为后件（箭头右部包含3）的规则均为低可信度的。
作用：利用上述性质来减少需要测试的规则数目

三、Aprior的算法实现

由于python的库暂无Aprior算法的实现模块，所以这里补充用python实现Aprior的代码：

#-*- coding:utf-8 -*-
from __future__ import print_function
import pandas as pd

#自定义连接函数,用于实现L_{k-1}到C_k的连接
def connect_string(x,ms):
    x=list(map(lambda i:sorted(i.split(ms)),x))
    l=len(x[0])
    r= []
    for i in range(len(x)):
        for j in range(i,len(x)):
            if x[i][:l-1] == x[j][:l-1] and x[i][l-1]!=x[j][l-1]:
                r.append(x[i][:l-1]+sorted([x[j][l-1],x[i][l-1]]))
    return r

#寻找关联规则的函数
def find_rule(d,support,confidence,ms=u'--'):
    result=pd.DataFrame(index=['support','confidence'])#定义输出结果

    support_series=1.0*d.sum()/len(d)#支持度序列
    column= list(support_series[support_series>support].index) #初步根据支持度筛选
    k=0

    while len(column) >1:
        k=k+1
        print(u'\n正在进行第%s次搜索...' %k)
        column = connect_string(column,ms)
        print(u'数目：%s...' %len(column))
        sf=lambda i:d[i].prod(axis=1,numeric_only=True) #新一批支持度的计算函数

        #创建连接数据，这一步耗时、耗内存最严重，当数据集较大时，可以考虑并行运算优化
        d_2 = pd.DataFrame(list(map(sf,column)),index=[ms.join(i) for i in column]).T

        support_series_2=1.0*d_2[[ms.join(i) for i in column]].sum()/len(d)#计算连接后的支持度
        column=list(support_series_2[support_series_2 > support].index) #新一轮支持度筛选
        support_series = support_series.append(support_series_2)
        column2=[]

        for i in column:#遍历可能的推理，如{A,B,C}究竟时A+B-->C还是B+C-->A还是C+A-->B?
            i = i.split(ms)
            for j in range(len(i)):
                column2.append(i[:j]+i[j+1:]+i[j:j+1])

        confidence_series=pd.Series(index=[ms.join(i) for i in column2])#定义置信度序列

        for i in column2:#计算置信度序列
            confidence_series[ms.join(i)] = support_series[ms.join(sorted(i))]/support_series[ms.join(i[:len(i)-1])]
    
        for i in confidence_series[confidence_series > confidence].index:
            #置信度筛选
            result[i]=0.0
            result[i]['confidence'] = confidence_series[i]
            result[i]['support']=support_series[ms.join(sorted(i.split(ms)))]

    result = result.T.sort_values(['confidence','support'],ascending=False)#整理结果，输出
    print(u'\n结果为:')
    print(result)

    return result