ROC曲线

本次学习我们将看看当一个机器算法模型训练完成后，如何使用ROC曲线来衡量它的好坏。会介绍混淆矩阵、ROC曲线如何生成。

一、混淆矩阵

对于二分类来说，混淆矩阵就分为四个模块：
结果为“真”的分对了就是True Positives；
结果为“真”的分错了就是False Positives；
结果为“假”的分对了就是True Negatives；
结果为“假”的分错了就是False Negatives；
这个还是比较容易混乱，大家就记住“True”就代表分队了，“False”就代表分错了.如下图所示，我们还能够获得fp rate、tp rate、precision、recall、accuracy、F-measure的计算过程：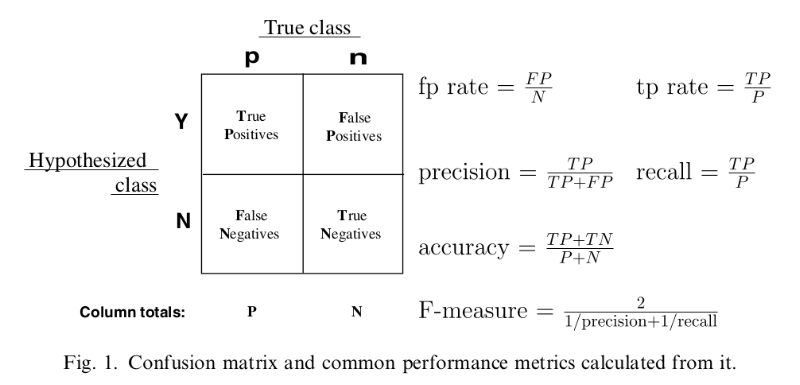

二、ROC曲线图

1、理解ROC

于是，由于：$FPrate=\frac{FP}{FP+TN}$，$TPrate=\frac{TP}{TP+FN}$，可画出下面的ROC曲线图：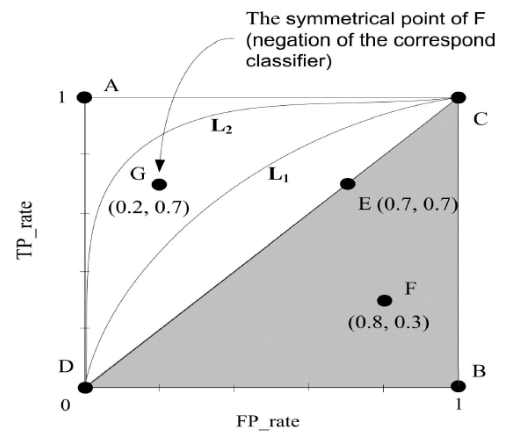

接下来我们来解释一下这个图：

<1>第一个点(0,1)，即FP_rate=0,TP_rate=1,这意味着FN（false negative）=0,并且FP（false positive）=0。这是一个完美的分类器，它将所有的样本都正确分类。

<2>第二个点(1,0)，即FP_rate=1,TP_rate=0,类似地分析可以发现这是一个最糟糕的分类器，因为它成功的避开了所有正确答案。

<3>第三个点(0,0)，即FP_rate=TP_rate=0，即FP（false positive）=TP（true positive）=0，可以发现该分类器预测所有的样本都为负样本（negative）

<4>第四个点(1,1)，分类器预测所有的样本都为正样本。
经以上分析，可以发现，ROC曲线越接近左上角，该分类器的性能越好。

问题：对于一个特定的分类器和测试数据集，显然只能得到一个分类混淆矩阵，即ROC线上的一个点，若要一系列的点怎么办？

2、绘制ROC

举个例子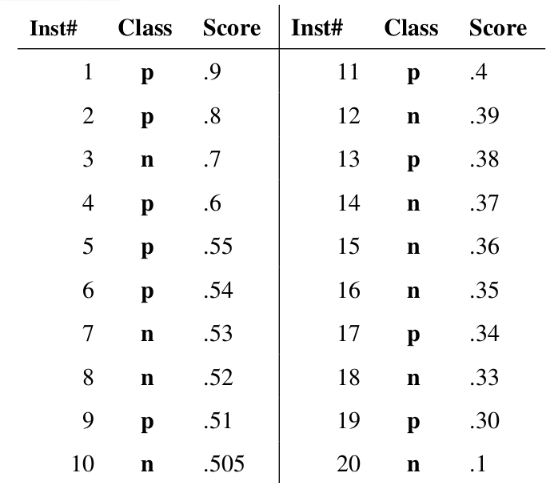

接下来，我们从高到低，依次将“Score”值作为阈值threshold，当测试样本属于正样本的概率大于或等于这个threshold时，我们认为它为正样本，否则为负样本。举例来说，对于图中的第4个样本，其“Score”值为0.6，那么样本1，2，3，4都被认为是正样本，因为它们的“Score”值都大于等于0.6，而其他样本则都认为是负样本。
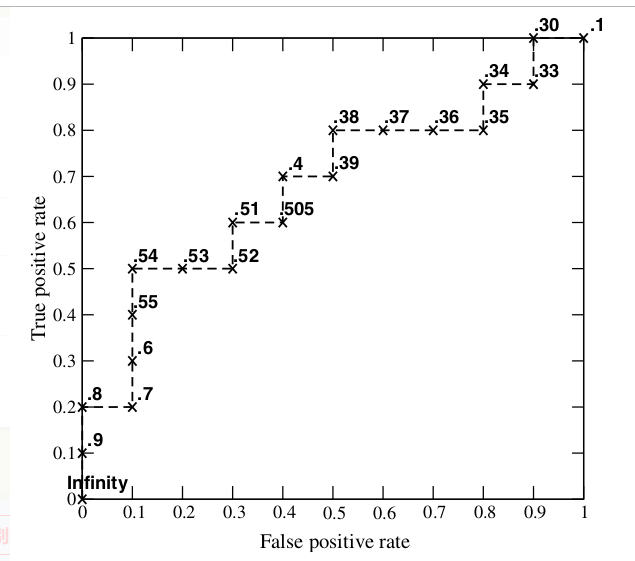
每次选取一个不同的threshold，我们就可以得到一组FPR和TPR，即ROC曲线上的一点。这样一来，我们一共得到了20组FPR和TPR的值
画出ROC图：