数据挖掘实战5-家用电器用户行为分析与事件识别

本次学习我们将沿用前面的数据挖掘过程，仍然处理一个分类问题，并着重学习一些新的数据处理手段。

问题背景：如果你是一个家电公司的，你要卖热水器，但是不同的地区气候、不同区域、用户的差别都会导致使用不同，你为了能因地制宜，因人而异的挣更多钱，你需要了解用户的热水器使用习惯。由于你们公司热水器能记录用户热水器的温度，开机，加热等状态数据，所以你获得了原始的一些热水器数据。

一、挖掘目标

1) 根据热水器采集到的数据，划分一次完整用水事件
2) 在划分好的一次完整用水事件中，识别出洗浴事件
这属于识别分类 0-1二分类问题与实践一中偷电用户的识别相类似，不过数据更难以处理。

二、数据抽取

1) 智能热水器在状态发生改变或者水流量非零时，每两秒会采集一条状态数据。
2) 本案例抽取200家热水器用户从2014年1月1日至2014年12月31日的用水记录。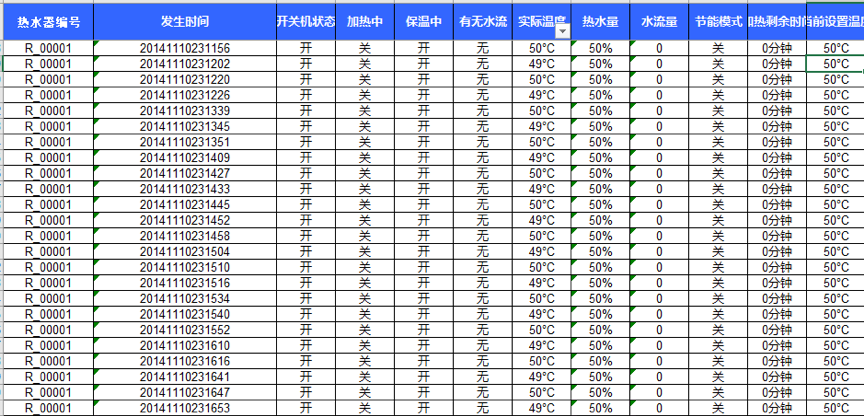

三、数据探索

用水停顿时间间隔为一条流量不为0的流水记录同下一条水流量不为0的流水记录之间的时间间隔。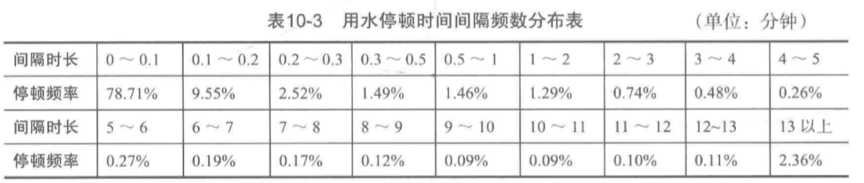

如上表可知，停顿时间间隔为0~0.3分钟的频率很高，根据日常用水经验可以判断为一次用水事件中的停顿；停顿时间为6~13分钟的频率较低，分析其为两次用水事件之间的停顿间隔。两次用水事件的停顿时间间隔分布在3~7分钟。

四、数据预处理

数据规约

1) 属性规约：去除“机器编号”、“有无水流”（水流量可以表示）、“节能模式”（都为关）
2) 数值规约：“开关机状态”为“关”且水流量为0时，说明热水器不处于工作状态，数据记录可以删除。

数据变换

本案例首先需要从原始记录中划分哪些连续的记录是一次完整的用水事件，一次完整的用水事件是根据水流量和停顿时间间隔的阈值去划分的，所以还建立阈值寻优模型。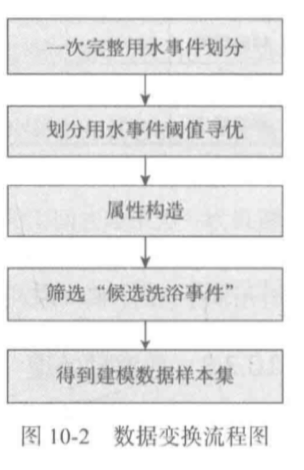

1) 一次完整用水事件的划分模型

在用水记录中，水流量不为0表示正在使用热水；水流量为0是用户用水发生停顿或者用水结束。如果水流量为0的记录之间的时间间隔超过一个阈值T，则划分为一个用水事件。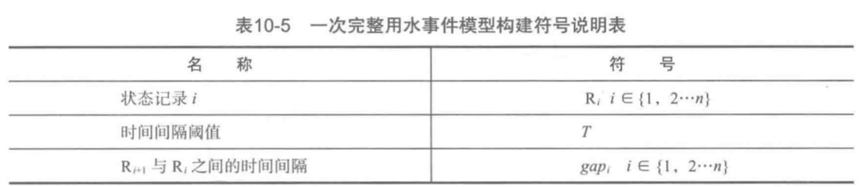

一次完整用水事件的划分步骤如下：

• 1）读取数据记录，识别到第一条水流量不为0的数据记录记为$R_1$，按顺序识别接下来的一条水流量不为0的数据记录$R_2$
• 2）若$gap_i>T$，则$R_{i+1}$与$R_i$及之间的数据记录不能划分到同一次用水事件。同时将$R_{i+1}记录作为新的读取数据记录的开始，返回步骤1）；若$gap_i<T$，则将$R_{i+1}$与$R_i$及之间的数据记录划分到同一次用水事件，并记录截接下来的水流了不为0数据记录为$R_{i+2}$
• 3）循环执行步骤2），直到数据记录读取完毕，结束事件划分。
  Python代码实现用水事件的划分：

  #-*- coding:utf-8 -*-
  #用水事件划分
  import pandas as pd
  
  threshold=pd.Timedelta(minutes=4) #阈值为4分钟
  inputfile='../data/water_heater.xls' #输入数据路径，需要使用excel格式
  outputfile='../tmp/dividsequence.xls' #输出数据路径，需要使用excel格式
  
  data=pd.read_excel(inputfile)
  data[u'发生时间']=pd.to_datetime(data[u'发生时间'],format='%Y%m%d%H%M%S')
  data=data[data[u'水流量']>0] #只要水流量大于0的记录
  d=data[u'发生时间'].diff()>threshold #相邻时间做差分，比较是否大于阈值
  data[u'事件编号']=d.cumsum()+1
  
  data.to_excel(outputfile)

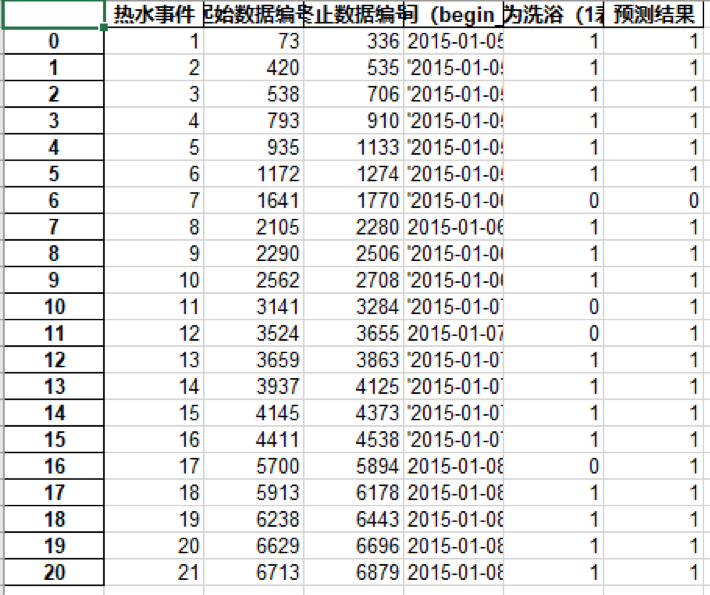
划分结果如下：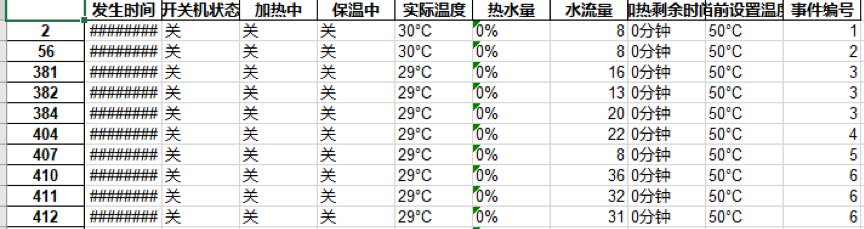

2) 用水事件阈值寻优模型

不同地区、不同人、不同季节用水习惯不相同，停顿时长不相同导致阈值差异，建立阈值寻优模型来更新寻找最优的阈值，将事件划分更加合理。

阈值事件个数在某个阈值区间内趋于稳定，可以取该段开始阈值（及其后4个点）进行斜率寻优。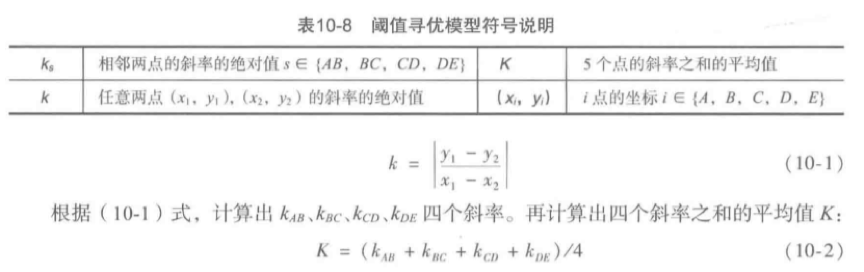

K可以作为A点的斜率指标。
于是，阈值优化过程如下：

当K<1，则取阈值最小的点A，把它的阈值作为划分事件的标准（其中1是专家阈值）
当不存在K<1是，则找所有阈值中斜率指标K最小的阈值；如果该最小K小于5，则取该阈值作为标准；若该最小K不小于5，则取专家默认阈值4分钟。

Python实现在1-9分钟内阈值寻优：

#-*- coding:utf-8 -*-
#阈值寻优
import numpy as np
import pandas as pd

inputfile='../data/water_heater.xls'#输入数据路径
n=4#使用以后4个点的平均斜率

threshold=pd.Timedelta(minutes=5) #专家阈值
data=pd.read_excel(inputfile)
data[u'发生时间']=pd.to_datetime(data[u'发生时间'],format='%Y%m%d%H%M%S')
data=data[data[u'水流量']>0] #只要水流量大于0的记录

def event_num(ts):
    d=data[u'发生时间'].diff()>ts #相邻事件做查分，比较是否大于阈值
    return d.sum()+1 #这样直接返回时间数

dt=[pd.Timedelta(minutes=i) for i in np.arange(1,9,0.25)]
h=pd.DataFrame(dt,columns=[u'阈值']) #定义阈值列
h[u'事件数']=h[u'阈值'].apply(event_num) #计算每个阈值对应的事件个数，阈值作为参数传禁区
h[u'斜率']=h[u'事件数'].diff()/0.25 #计算每两个相邻点对应的斜率，每两个相邻点相差0.25
h[u'斜率指标'] =h[u'斜率'].abs().rolling(n).mean() #采用后n个斜率的绝对值平均作为斜率指标

ts=h[u'阈值'][h[u'斜率指标'].idxmin()-n]
#注：用idmin返回最小值的index，由于rolling_mean()自动计算的是前n个斜率的绝对值平均
#所以结果要进行平移（-n）

if ts>threshold:
    ts=pd.Timedelta(minutes=4)

print(ts)

寻优结果如下：

0 days 00:04:00

最优阈值4分钟

3）属性构造

本案例研究的是用水行为，可以构造4类指标来进行模型的训练：时长指标、频率指标、用水的量化指标以及用水的波动指标，计算如下：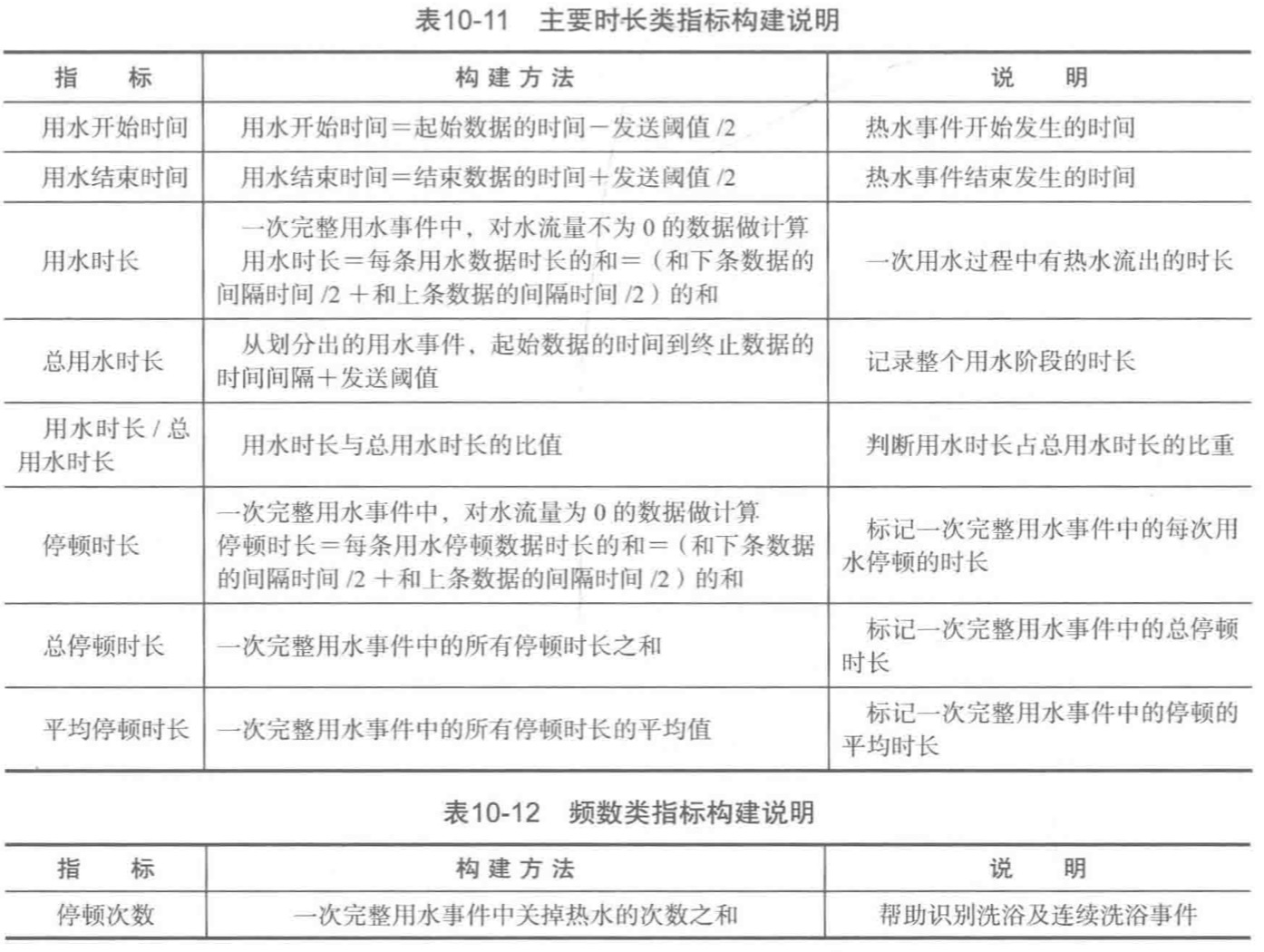

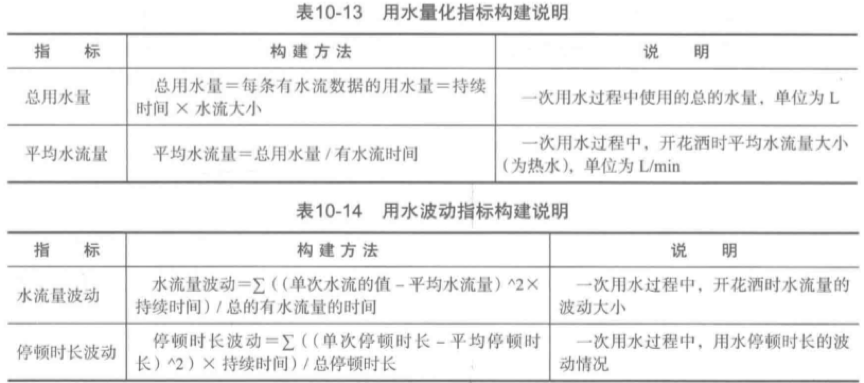
4) 筛选得“候选洗浴事件”

首先，用3个比较宽松的条件筛选掉哪些非常短暂的用水事件：

• 一次用水事件中总用水量（纯热水）小于y升
• 用水时长小于100秒
• 总用水时长小于120秒
  其次，对y的合理取值进行探究。
  
  

数据清洗

一次完整的用水事件，需要一个开始用水的状态记录和结束用水的状态记录。但是，在划分一次完整用水事件时，发现数据中存在没有结束用水的状态情况。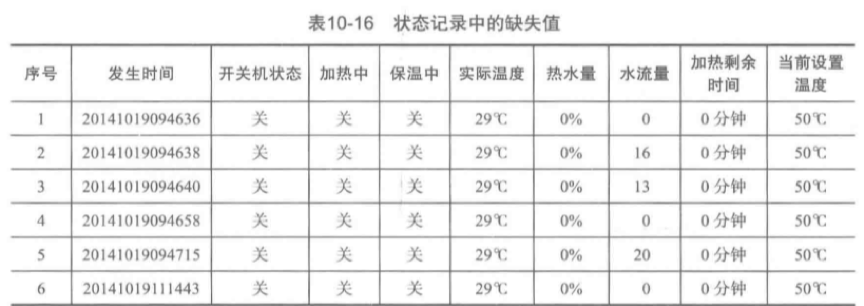

如图，第5条状态和第7条状态记录的事件间隔应为2秒，而表中间隔太大。
该类缺失值的处理如下：
在存在用水状态记录缺失的情况下，填充一条状态记录使水流量为0，发生时间加2秒，其余属性状态不变。

五、模型构建

本次使用多层神经网络，详情介绍请点击神经网络算法,建模样本数据如下：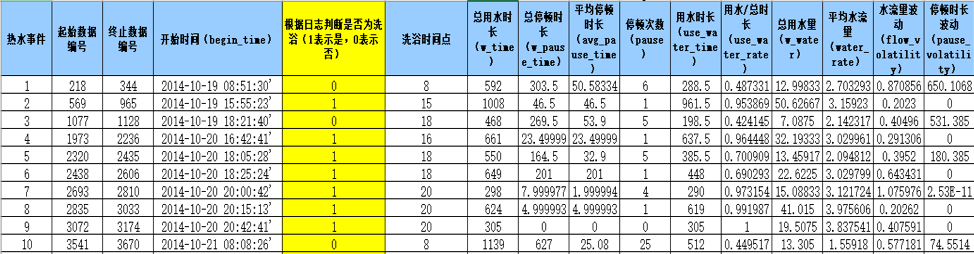

模型选择：11个属性作为输入，含有两个隐含层的神经网络，隐节点数分别为17，10时训练最优，输出为1表示为洗浴事件，输出为0表示不是洗浴事件。

Python实现多层神经网络代码：

#-*- coding:utf-8 -*-
#建立、训练多层神经网络，并完成模型的检验
from __future__ import print_function
import pandas as pd

inputfile1='../data/train_neural_network_data.xls' #训练数据
inputfile2='../data/test_neural_network_data.xls' #测试数据
testoutputfile='../tmp/test_output_data.xls' #测试数据模型输出文件
data_train=pd.read_excel(inputfile1) #读入训练数据（由日志标记时间是否为洗浴）
data_test=pd.read_excel(inputfile2) #读入测试数据（有日志标记时间是否为洗浴）
y_train=data_train.iloc[:,4].as_matrix() #训练样本标签列
x_train=data_train.iloc[:,5:17].as_matrix() #训练样本特征
y_test=data_test.iloc[:,4].as_matrix() #测试样本标签列
x_test=data_test.iloc[:,5:17].as_matrix() #测试样本特征

from keras.models import Sequential
from keras.layers.core import Dense,Dropout,Activation

model = Sequential() #建立模型
model.add(Dense(input_dim=11,output_dim=17))#添加输入层、隐藏层的连接
model.add(Activation('relu')) #以Relu函数为激活函数
model.add(Dense(input_dim=17,output_dim=10)) #添加隐藏层、隐藏层的链接
model.add(Activation('relu')) #以Relu函数为激活函数
model.add(Dense(input_dim=10,output_dim=1))  #添加隐藏层、输出层的连接
model.add(Activation('sigmoid')) #以sigmoid函数为激活函数

#编译模型，损失函数为binary_crossentropy,用adam法求解
model.compile(loss='binary_crossentropy',optimizer='adam',metrics=['accuracy'])

model.fit(x_train,y_train,nb_epoch=100,batch_size=2) #训练模型 batch=2时准确率85.7
model.save_weights('../tmp/net.model') #保存模型参数
'''
#导入训练好的model weights
weight_file='../tmp/net.model'
model.load_weights(weight_file)
'''
r=pd.DataFrame(model.predict_classes(x_test),columns=[u'预测结果'])
pd.concat([data_test.iloc[:,:5],r],axis=1).to_excel(testoutputfile)
model.predict(x_test)

六、模型评价

该模型预测结果比较如下，总共识别了21条数据，准确识别了18条数据，正确率为85.7%